P′′
P′′ is a primitive computer programming language created by Corrado Böhm[1][2] in 1964 to describe a family of Turing machines.
Contents |
Definition
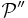 (hereafter written P′′) is formally defined as a set of words on the four-instruction alphabet {R, λ, (, )}, as follows:
(hereafter written P′′) is formally defined as a set of words on the four-instruction alphabet {R, λ, (, )}, as follows:
Syntax
- R and λ are words in P′′.
- If p and q are words in P′′, then pq is a word in P′′.
- If q is a word in P′′, then (q) is a word in P′′.
- Only words derivable from the previous three rules are words in P′′.
Semantics
- {a0, a1, ..., an}(n ≥ 1) is the tape-alphabet of a Turing machine with left-infinite tape, a0 being the blank symbol.
- R means move the tape-head rightward one cell (if any).
- λ means replace the current symbol ai by ai+1 (taking an+1 = a0), and then move the tape-head leftward one cell.
- (q) means iterate q in a while loop, with condition that the current symbol is not a0.
- A program is a word in P′′. Execution of a program proceeds left-to-right, executing R, λ, and (q) as they are encountered, until there is nothing more to execute.
Relation to other programming languages
- P′′ was the first "GOTO-less" imperative structured programming language to be proven1,2 Turing-complete.
- The brainfuck language (apart from its I/O commands) is a minor informal variation of P′′. Böhm1 gives explicit P′′ programs for each of a set of basic functions sufficient to compute any computable function, using only (, ) and the four words r ≡ λR, r′ ≡ rn (rn means rrrrr...rr [n times]), L ≡ r′λ, R. These are the equivalents of the six respective brainfuck commands [, ], +, -, <, >. Note that since an+1 = a0, performing r ("increment" symbol in current cell) n times will wrap around so that the result is to "decrement" the symbol in the current cell by one (r′).
Example program
Böhm1 gives the following program to compute the predecessor (x-1) of an integer x > 0:
R ( R ) L ( r' ( L ( L ) ) r' L ) R r
which translates directly to the equivalent brainfuck program
> [ > ] < [ − [ < [ < ] ] − < ] > +
The program expects an integer to be represented in bijective base-n notation, with a1, ..., an coding the digits 1,...,n, respectively, and to have an a0 before and after the digit-string. (E.g. in bijective base-2, the number eight would be encoded as a0a1a1a2a0, because 8 = 1*22 + 1*21 + 2*20.) At the beginning and end of the computation, the tape-head is on the a0 preceding the digit-string.
References
- ^ Böhm, C.: "On a family of Turing machines and the related programming language", ICC Bull. 3, 185-194, July 1964.
- ^ Böhm, C. and Jacopini, G.: "Flow diagrams, Turing machines and languages with only two formation rules", CACM 9(5), 1966. (Note: This is the most-cited paper on the structured program theorem.)